こんにちは、ふくろうです。
あざらしがフライト訓練前に、携帯でGround SpeedとWind Correction Angleを自動計算アプリで計算しているのを見かけました。最近は何でも携帯アプリで自動計算出来るようになっており便利です。ただ、アプリ内の自動計算がどのようになされているか、そのブラックボックスの中身が知りたいため、考えてみました。
Ground Speed, Wind Correction Angleとは
飛行機が進もうとする目的の方向に対して、風が影響した結果、飛行機の進む方向が変化してしまいます。
飛行機の計器には、風に影響された結果としての飛行機の進む方向(Course)と、風の影響が反映されていない飛行機速度(True Air Speed)が表示されます。
目的地への最短飛行ルートと目的地までの飛行時間を求めるためには、Ground Speed(計器表示と風の影響を考慮した対地速度)と、Wind Correction Angle(風の影響を考慮した修正角度)を計算し、飛行機の操作へ反映する必要があります。
Ground Speed, Wind Correction Angleの図解
いきなり計算方法に進む前に、まずは飛行機と風、その合力を絵にすることで、上記文章のイメージを得ます。ここでは、中学で学んだベクトル合成を使用します。
<条件>
- 飛行機の計器表示:True Air Speed
- 飛行機のコンパス:Course
- 風の向き:Wind
- 風速
これを図にすると例えば以下になります。ベクトル(矢印)の長さは速度の大きさを表します。
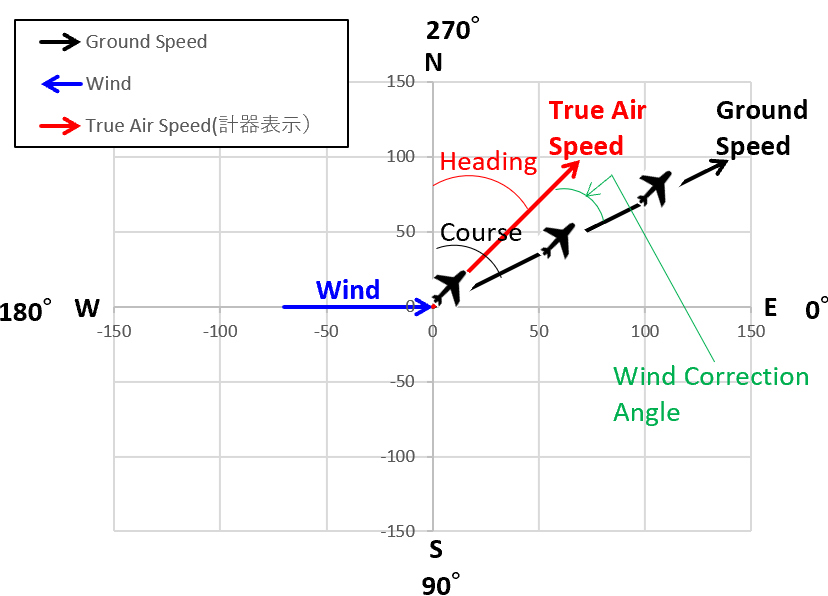
飛行機は風の影響を受けて飛行しているので、目的のHeadingに機首を向けつつも、Course方向にGround Speedで進むことになります。
ベクトルで考えれば、Ground SpeedはTrue Air SpeedとWindの合力です。Wind Correction AngleはCourseとHeadingの角度差になります。
Ground Speedを求める
Ground Speed計算にあたり、各要素を記号化します。
- 飛行機の計器表示:True Air Speed:x (kt)
- 飛行機のコンパス:Course:Y (deg)
- 風の向き:Wind:Z (deg)
- 風速:z (kt)
- Ground Speed: y (kt)
上記の図と同じものを抜粋しています。
Course Y(deg)とWind Z(deg)が成す角度が算出でき、180-(Y-Z)となります。
*解の公式を使用するのでY-Zで計算しても構いません
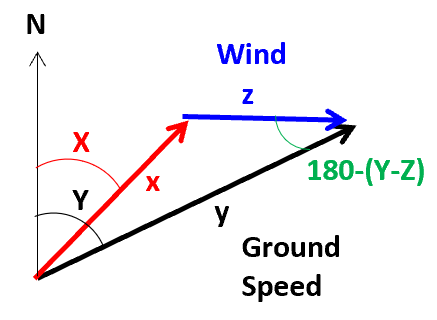
三角形の余弦定理を使用します。
x2 = z2 + y2 -2zycos(180-(Y-Z))
Ground Speed: yを求めたいのでyでまとめます。
y2 + (-2zcos(180-(Y-Z))y + (z2 - x2) = 0
解の公式を使用してyを求めます。Ground Speed: yは±の2つの解を得ます。
y = (-(-2zcos(180-(Y-Z)))±√((-2zcos(180-(Y-Z)))2 -4(z2 - x2))) / 2
風の向きZと飛行機のコンパスYの角度により、2つの解のどちらかを選択します。例えば飛行機のコンパスYの角度に±90deg以内の方向に風の向きZが向いていれば、+を選択します。
これでGround Speed: y(kt)が算出できました。
Wind Correction Angleを求める
先ほどと同じ図を載せます。
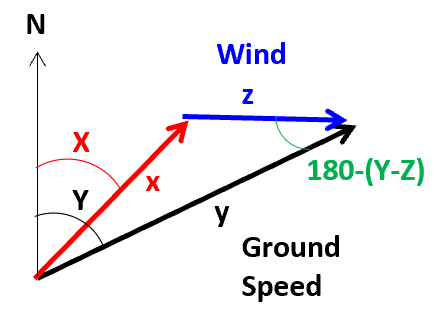
(Y-X)が機首とCourseとの角度差になり、これがWind Correction Angleです。
余弦定理を使用します。(Y-X)で計算をまとめると、その解がWind Correction Angleとなります。
cos(Y-X) = (x2 + y2 -z2) / (2xy)
(Y-X) = cos-1((x2 + y2 -z2) / (2xy))
これでWind Correction Angle(deg)が算出できました。
計算例
以下に例としての数字を示します。
飛行機が西北西に進もうとしていますが、風が北向きに吹いているため、飛行機が北西に流されている状況です。
- 飛行機の計器表示:True Air Speed:x=120 (kt)
- 飛行機のコンパス:Course:Y=325 (deg)
- 風の向き:Wind:Z=180 (deg)
- 風速:z=70 (kt) *強風
- Ground Speed: y (kt)
- Wind Correction Angle:(Y-X) (deg)
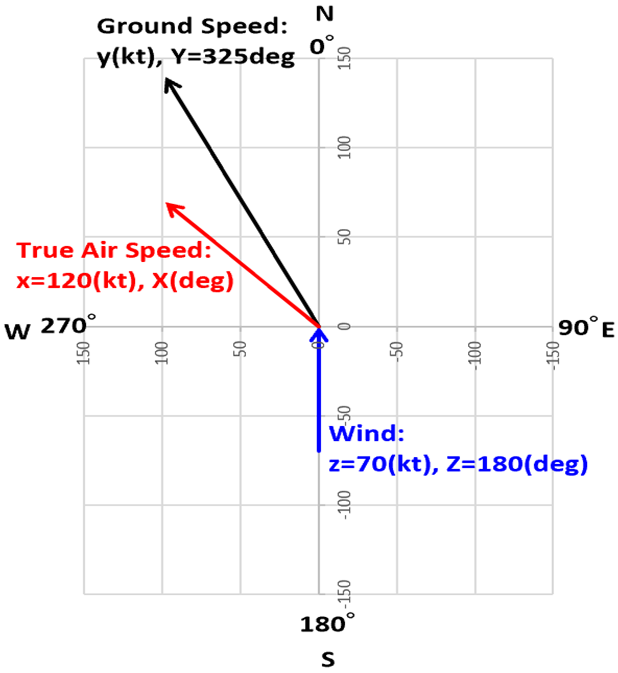
先の計算式を引用します。
- y = (-(-2zcos(180-(Y-Z)))±√((-2zcos(180-(Y-Z)))2 -4(z2 - x2))) / 2
- (Y-X) = cos-1((x2 + y2 -z2) / (2xy))
上記計算式に数字を入力します。
- y = (-(-2*70*cos(180-(325-180)))±√((-2*70*cos(180-(325-180)))2 -4*(702 - 1202))) / 2
- (Y-X) = cos-1((1202 + y2 -702) / (2*120*y))
以下が解になります。エクセルで計算する際はラジアン変換に注意ください。
- y = 170.4 (kt)
- (Y-X) = 20 (deg)※左へ
これでフライトコンピュータが破損したときも、焦らずに手計算できますね!
どうもあざらしです。おまけでE6-Bで求めてみます。但し、前述の風速はセスナが空中分解の危機に瀕するほどの強さなので、少々変更します。
※E6-Bでは最高でも50KTまでしか計算できません。
- 飛行機の計器表示:True Air Speed:x=120 (kt)
- 飛行機のコンパス:Course:Y=325 (deg)
- 風の向き:Wind:Z=180 (deg)
- 風速:z=20 (kt)
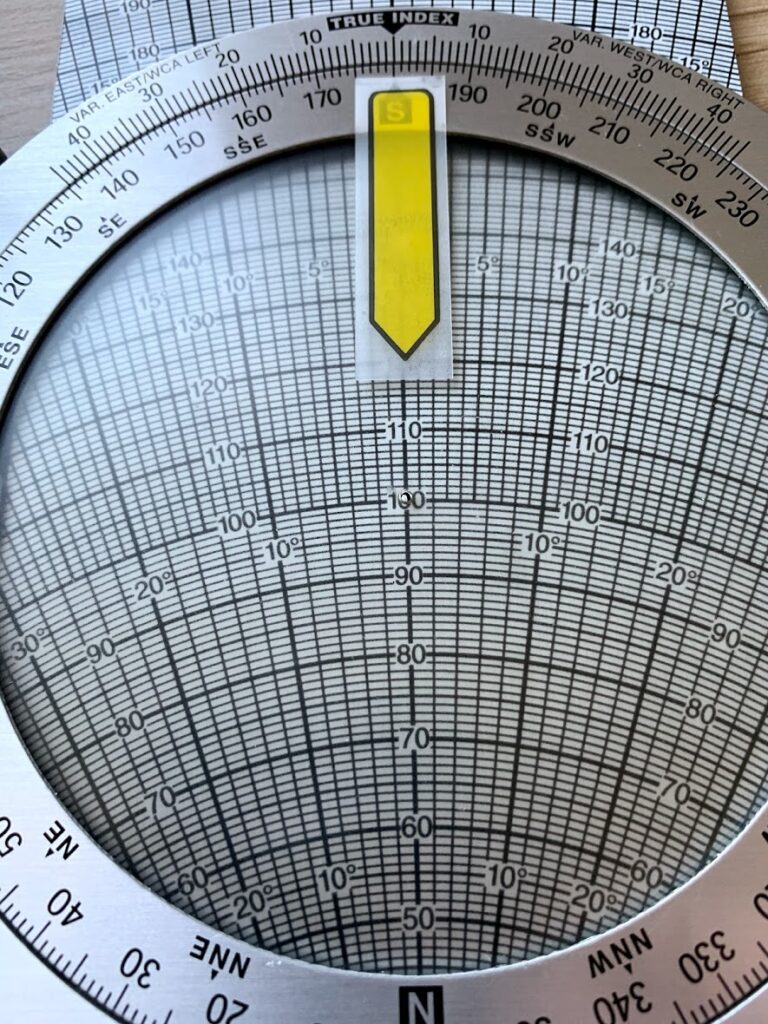
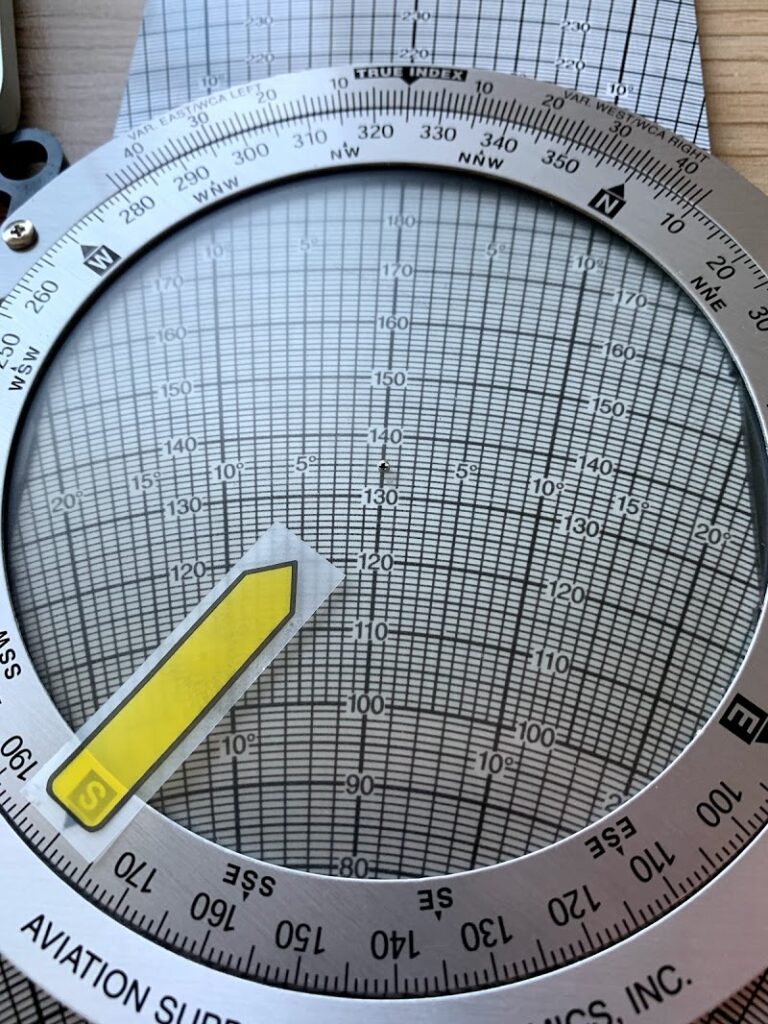
まず風向を合わせ、中心基準は100に。風速は20なので、120の場所に付箋を貼る。
次に、コンパスのHDG(heading)325にベゼルをセット
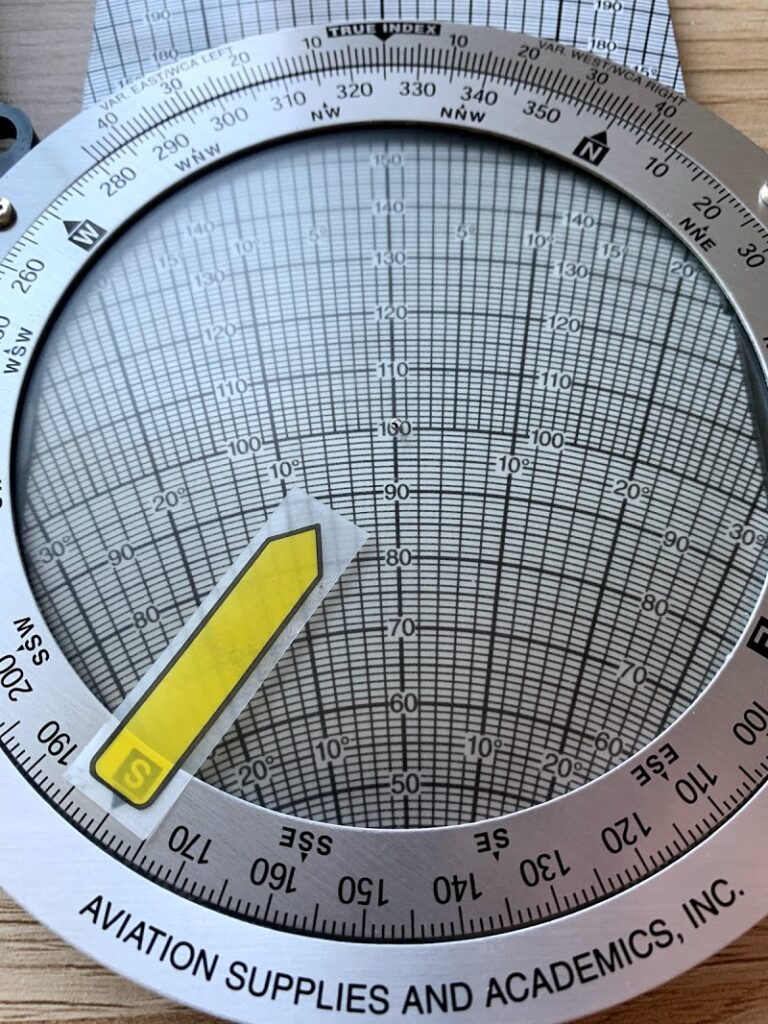
付箋の部分を120の弧へ当てる。
あとは数字を読むだけ☆
Ground speed:135KT
WCA:-5°(左)
簡単ですね。フクロウが隣のデスクで「あーでもない、こーでもない!」と頑張ってExcelに数式入力しているのを、アプリとE6-B片手に生ぬるい目で見守っていました。
文明の力ですね。
ではでは